2015-06-21

次元削除 ( t-SNE )

機械学習

　今回は、kaggle のOtto Group Production Classification Challenge の上位の方々が次元削除の手法としてt-SNE(t-distributed stochastic neighbor embedding) を使用されていたので調べてみようと思いました。個人的には、pca(主成分分析) ぐらいしか思い付かなかったのですが、それぞれ比較しながら見ていきます。
t-sne の詳細についてこちらを参考にするといいかと思います。
http://jmlr.org/papers/volume9/vandermaaten08a/vandermaaten08a.pdf
こちらに書かれているようにt-SNE は高次元のものを2 または3 次元に写像するように作られています。とりあえず、R のtsne package を試してみます。(あとでより高速なRtsne package を用います)

library(tsne)
colors = rainbow(length(unique(iris$Species)))
names(colors) = unique(iris$Species)
set.seed(1)
iris.tsne = tsne(iris[,1:4], max_iter=200) # 時間短縮のため max_iter=200
plot(iris.tsne, t='n', main="tsne")
text(iris.tsne, labels=as.integer(as.factor(iris$Species)), col=colors[iris$Species])

# PCA と比較
dev.new()
iris.pca = princomp(iris[,1:4])$scores[,1:2]
plot(iris.pca, t='n', main="pca")
text(iris.pca, labels=as.integer(as.factor(iris$Species)),col=colors[iris$Species])

これを実行すると次のような図を得ます。
まず、t-sne
f:id:puyokw:20150620094617j:plain
次に、pca
f:id:puyokw:20150620234024j:plain
これを見た感じだとpca の方が良さそうです。
　次に、先ほどの例ではt-SNE の良さがあまり分からなかったので、別の例として手書き文字(数字)の認識を例としてみていきたいと思います。t-SNE とpca を比較したスクリプトがkaggle の"script of the week" で取り上げていただきました！ので、そちらにリンクを張っておきます。
https://www.kaggle.com/puyokw/digit-recognizer/clustering-in-2-dimension-using-tsnewww.kaggle.com
結果はこのようになっています。
t-sne
f:id:puyokw:20160522131238p:plain
pca
f:id:puyokw:20160522131256p:plain
こちらでは、t-SNE がかなりきれいにクラス分類されているのが分かります。ただこの場合でも、pca はダメという分けではなく、単にどのような処理をしたいかに合わせてpca とt-SNE を選択する必要があるということです。

　R にはt-SNE の高速版のRtsne package があり、これは主成分分析をしてからt-SNE を実行します(prcomp を使用しています)。
　Rtsne についての論文はこちらになります。
http://arxiv.org/pdf/1301.3342v2.pdf
上記のページが意外と重かったので、アブストが書かれているページにもリンクしておきます。
[1301.3342] Barnes-Hut-SNE
ここに書かれているように、この方法は Barnes-Hut-SNE と呼ばれていてこのアルゴリズムではO(nlogn) で実行できます。元のアルゴリズムはO(n^2) です。これはvantage-point trees やBarnes-Hut のアルゴリズムを使用しています。　使い方はtsne とほぼ同じ感じです。

library(Rtsne)
set.seed(1) # 再現性の確保
# verbose=TRUE で途中経過が出力されます
iris.tsne <- Rtsne(as.matrix(iris[,1:4]), check_duplicates = FALSE, verbose=TRUE)
colors = rainbow(length(unique(iris$Species)))
plot(iris.tsne$Y, t='n', main="Rtsne")
text(iris.tsne$Y, labels=as.integer(as.factor(iris$Species)), col=colors[iris$Species])

　Rtsne のパラメータ中にtheta(=0.5 :default) が含まれています(上記のコードには入れていません)が、これを0 に近づけるほど精度は良くなりますがその代わりに実行時間が長くなります。

追記(2016/06/04)
一応、python での例も載せておきます。

import numpy as np
import pandas as pd
from sklearn.manifold import TSNE
from sklearn import datasets
import matplotlib.pyplot as plt

# import iris data 
iris = datasets.load_iris()
X = iris.data
Y = iris.target

model = TSNE(n_components=2, perplexity=50, n_iter=500, verbose=3, random_state=1)
X = model.fit_transform(X)

# Plot the points
plt.figure(2, figsize=(8, 6))
plt.clf()
plt.scatter(X[:, 0], X[:, 1], c=Y, cmap=plt.cm.Paired)
plt.xlabel('tsne1')
plt.ylabel('tsne2')
plt.show()

追記(2016/05/23)
t-sne の利点:
他の視覚化よりも綺麗に図示されることが多い。(特にクラス分類)

t-sne の欠点:
計算に非常に時間がかかる
メモリの消費量が多い(特に、python)

kaggle における実例：
otto: Otto Group Product Classification Challenge | Kaggle
digit recognizer(上記のもの): Digit Recognizer | Kaggle
spring leaf marketing response(コードのみ): Solution Sharing - Springleaf Marketing Response | Kaggle

こちらのサイトに有名なデータセットに対するいくつかの例がExmaples の項目に載っています。t-SNE – Laurens van der Maaten

追記(2015/08/02)：実際に、t-SNE で3次元にしたものと元のデータを結合してrandomForest などを用いたコード(kaggle のdigit recognizerで用いたもの)をgithub 上にupload しました。精度は若干向上します。
GitHub - puyokw/kaggle_digitRecognizer: Scripts for digit Recognizer in kaggle

2015-04-29

Xgboost のR における具体例 (クラス分類)

xgboost 機械学習

前回、Xgboost のパラメータについて列挙しましたが、あれだけ見ても実際にどう使うのかよく分かりません。そこで今回はR で、とりあえず iris data を用いてその使い方を見ていきたいと思います。
　まず、iris data の奇数番目を訓練データ、偶数番目を検証データとします。

dim(iris) # 行数:150, 列数:5
odd.n<-2*(1:75)-1
iris.train<-iris[odd.n,] # 奇数を訓練データ
iris.test<-iris[-odd.n,] # 偶数を検証データ

　次に、xgboost に適した形式に変換します。

library(xgboost)
y <- iris.train[,5] # 目的変数
y <- as.integer(y)-1 #xgboost で既定されいるクラスは 0 base

train.x<-iris.train[,1:4]
x <- rbind(train.x,iris.test[,-5]) # xgboost を使うときのため
x <- as.matrix(x)

trind <- 1:length(y) # 先程定義したx の中の訓練データを指すのに使う
teind <- (nrow(train.x)+1):nrow(x) # 先程定義したx の中の検証用データを指すのに使う

必要最低限のパラメータの設定は次のようになります。

set.seed(131) # 固定シードで試す
param <- list("objective" = "multi:softprob", # 多クラスの分類で各クラスに所属する確率を求める
              "eval_metric" = "mlogloss", # 損失関数の設定
              "num_class" = 3 # class がいくつ存在するのか
              )

　実際に、予測をする前に最適な木の数を探します。

k<-round(1+log2(nrow(train.x)))
cv.nround <- 100 #search
bst.cv <- xgb.cv(param=param, data = x[trind,], label = y,  nfold = k, nrounds=cv.nround)

　これを実行すると、次のような結果が出てきます。

[0]     train-mlogloss:0.752857+0.007342        test-mlogloss:0.772249+0.027355
[1]     train-mlogloss:0.542712+0.008457        test-mlogloss:0.569818+0.047944
[2]     train-mlogloss:0.404424+0.008669        test-mlogloss:0.441932+0.068164
[3]     train-mlogloss:0.306743+0.007542        test-mlogloss:0.351062+0.084861
                                          (略)
[25]    train-mlogloss:0.032532+0.003092        test-mlogloss:0.122064+0.128217
[26]    train-mlogloss:0.031981+0.002944        test-mlogloss:0.121880+0.128820
[27]    train-mlogloss:0.031499+0.002809        test-mlogloss:0.121960+0.128635
                                          (略)
[97]    train-mlogloss:0.023760+0.001694        test-mlogloss:0.134890+0.156262
[98]    train-mlogloss:0.023744+0.001690        test-mlogloss:0.135084+0.156458
[99]    train-mlogloss:0.023728+0.001686        test-mlogloss:0.135296+0.156967

この場合、訓練データにおける最適な木の数は26+1(0 baseのため)となります。
これを基に予測をしてみます。

set.seed(131)
nround <- 27
# モデルの構築
bst <- xgboost(param=param, data = x[trind,], label = y, nrounds=nround)
pred <- predict(bst,x[teind,]) # モデルを使って予測値を算出
pred <- matrix(pred,3,length(pred)/3) # 今回は3クラスあるので
pred <- t(pred)
colnames(pred)<-c("setosa","versicolor","virginica")

　結果を見てみると、

head(pred,3)
        setosa  versicolor   virginica
[1,] 0.9838002 0.008915161 0.007284546
[2,] 0.9870363 0.008944485 0.004019236
[3,] 0.9870363 0.008944485 0.004019236

となっていて、各データが"setosa","versicolor","virginica"のどれに属するかの確率が求められています。この中の最大値をとるクラスに、そのデータは属すると思われます。
このような確率に興味がなく、どこのグループに属するかだけを知りたいなら次のように"multi:softmax"を使います。

param <- list("objective" = "multi:softmax", # multi:softmax に変更！
                "eval_metric" = "mlogloss", 
                "num_class" = 3 
                )
set.seed(131)
nround <- 27
bst <- xgboost(param=param, data = x[trind,], label = y, nrounds=nround)
pred <- predict(bst,x[teind,])

データを整えて、結果を見てみます。

for(i in 1:length(pred)){
  if(pred[i]==0) {pred[i]="setosa"}
  else if(pred[i]==1) {pred[i]="versicolor"}
  else {pred[i]="virginica"}
}
table(iris.test[,5],pred)
# 結果
            pred
             setosa versicolor virginica
  setosa         25          0         0
  versicolor      0         23         2
  virginica       0          0        25

これが良いのかどうかいまいち分からないので、とりあえずランダムフォレストと比較してみます。

odd.n<-2*(1:75)-1
iris.train<-iris[odd.n,] # 奇数を訓練データ
iris.test<-iris[-odd.n,] # 偶数を検証データ
# randomForest
library(randomForest)
set.seed(131)
train.x<-iris.train[,1:4]
train.y<-as.factor(iris.train[,5])
model.rf<-tuneRF(train.x,train.y,doBest=T)
pred<-predict(model.rf,iris.test[,-5])
table(iris.test[,5],pred)
# 結果
            pred
             setosa versicolor virginica
  setosa         25          0         0
  versicolor      0         24         1
  virginica       0          2        23

これだけでは、なんとも言えなさそうですが、xgboost の性能の高さは認めらるかなと思います。
追記(2015/05/06): 変数重要度を求めることができることに気が付いたので追記しておきます。

# 変数重要度を求める
imp<-xgb.importance(names(iris),model=bst)
print(imp)
# print の結果
        Feature        Gain      Cover Frequence
1: Petal.Length 0.663081352 0.63384270 0.4453125
2:  Petal.Width 0.318246635 0.24789925 0.2656250
3: Sepal.Length 0.011982305 0.09317686 0.2187500
4:  Sepal.Width 0.006689708 0.02508119 0.0703125
# print の結果ここまで
xgb.plot.importance(imp) # これをグラフで表示

変数重要度を図示したものがこちらになります。
f:id:puyokw:20150506003611j:plain
ランダムフォレストで変数重要度がどうなるのかも気になるので試してみます。

# 変数重要度を求める(和が1になるように調整)
print( model.rf$importance /sum(model.rf$importance) )
# print の結果
             MeanDecreaseGini
Sepal.Length       0.01306678
Sepal.Width        0.01388757
Petal.Length       0.42804382
Petal.Width        0.54500183
# print の結果ここまで
varImpPlot(model.rf) # 図示(略)

xgboost とランダムフォレストでずいぶん変数重要度が異なっていました。異なる基準を採用しているのかまでは、まだ調べられていません。(分かり次第また更新しようと思います。)

追記(2015/6/22): 決定木ベースの手法なので、決定木も出力できた方が良いかと思ったので、追記しておきます。

# 決定木を表示
xgb.plot.tree(feature_names=names(iris[,-5]),model=bst, n_first_tree=2)

これを実行すると次のような図がhtml 形式のファイルで出力されます。
f:id:puyokw:20150622013114p:plain

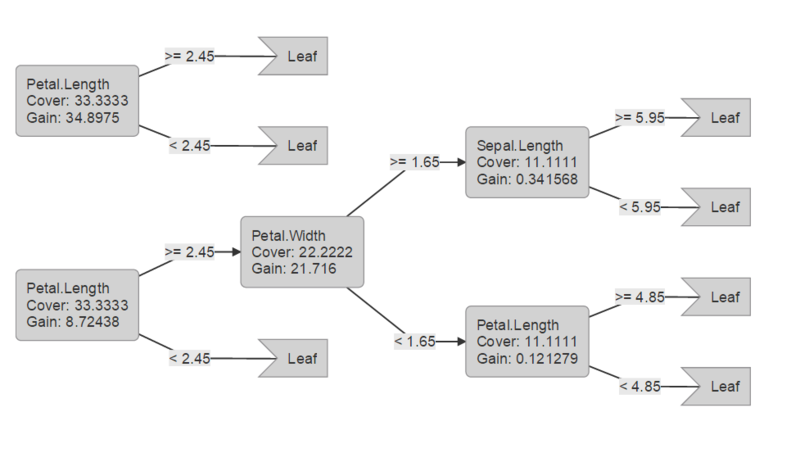
追記(2016/11/14): xgb.plot.tree を実行しても木が出力されないエラーに遭遇したのでコメントを付記しておきます。現在cran にあるパッケージではエラーがでるようでgithub からインストールすれば、正しく木が表示されました。

追記(2015/04/30)：今回使用したコードはpublic gist にup しておきます。
introduction to xgboost · GitHub
今回用いたiris のデータでは、パラメータ調整してもほとんどその効果が見られないため、改めて別のデータで試してみるか検討してみます。(やる場合にはGW中にup する予定です)　2015/04/30 0:40 追記

2015-04-11

xgboost のパラメータ

xgboost 機械学習

xgboost を使う上で、日本語のサイトが少ないと感じましたので、今回はパラメータについて、基本的にこちらのサイトの日本語訳です。

&amp;amp;amp;amp;lt;a href="https://github.com/dmlc/xgboost/wiki/Parameters" data-mce-href="https://github.com/dmlc/xgboost/wiki/Parameters"&amp;amp;amp;amp;gt;dmlc/xgboost&amp;amp;amp;amp;lt;/a&amp;amp;amp;amp;gt;github.com

xgboost を実行する前に、共通変数、ブースター変数、タスク変数の３つをセットしなければなりません。

共通変数は、木あるいは線形モデルのブースティングモデルに共通の変数です
ブースター変数は、木あるいは線形モデルの各々に固有の変数です
タスク変数は、どのように学習させるかを決めるもので、例えば、回帰タスクではランキングタスクの変数が異なっています
この３つの変数に加えて、コンソール変数があり、これはxgboost のコンソール版の動作に関連しています。(たとえば、作製したモデルを保存するときなど)

Rパッケージにおける変数

R のパッケージでは、. (ドット) を_ (アンダーバー)に置き換えて利用できます。例えば、max.depth はmax_depth とすると使えます。

共通変数

booster [デフォルト=gbtree]
- gbtree もしくは gblinear のいずれのブースターを使うかを決めます。詳細はこちらにあります(英語: Boosters · dmlc/xgboost Wiki · GitHub ) 。
silent [デフォルト=0]
- 0 にすると起動中のメッセージを出力し、1 にすると出力しません

nthread [設定しなければ、デフォルト値として使用可能なスレッドの最大数になります]
- xgboost を使用時の並列処理を行うスレッドの数

num_pbuffer [xgboost が自動的に設定するため、ユーザーが設定する必要はありません]
- 予測バッファのサイズで、たいていトレーニングデータ数で設定されます。ブースティングの最後の段階で予測の結果を保存するために使用されます。
num_feature [xgboost が自動的に設定するため、ユーザーが設定する必要はありません]
- ブースティングに使用する特徴次元の数で、その特徴次元の最大数に設定されます

ブースター変数

xgboost-unity より、接頭辞 bst: はブースター変数に付けなくても大丈夫です。変数に接頭辞 bst: を付けても付けなくても同じです。(たとえば、 bst:eta も eta も正しい変数で同じものを指しています)

木ブースター固有の変数

eta [default=0.3]
- ステップサイズの縮小幅で、オーバーフィッティングを防ぐために使用されます。各ブースティングのステップ終了後に、新しい特徴の重みを直接入手できます。そして eta　は特徴の重みを縮小させてブースティングの過程をより強固なもの*1にします。

ここで、強固と使っている意味は、外れ値に強くなるという意味と汎化性能が低くなるという意味の両方を込めています(良い点と悪い点)。以下も同様です。

gamma
- 損失還元(loss reduction)の最小値で、木の葉ノードをさらに分割する際に必要な値。値を大きくすると、そのアルゴリズムはより強固になります。
max_depth [default=6]
- 木の深さの最大値
min_child_weight [default=1]
- 子ノードにおける必要な最小の重み。木の分割段階で、ある葉ノードにおける重みの合計値がmin_child_weight 未満であれば、それ以上分割しません。たとえば線形回帰の場合には、各ノードに必要な例の最小値に対応しています。値を大きくするとそのアルゴリズムはより強固になります。
max_delta_step [default=0]
- 値を0に設定した場合、特になにもしません。もし正の値にした場合には、ステップの更新でより強固に(柔軟性がない) します。このパラメータは必要でないことが多いが、クラスのバランスが著しく悪いときのロジスティック回帰で役立つかもしれません。値を1～10に設定すると良いでしょう。
subsample [default=1]
- サブサンプルを生成する際のトレーニングデータの抽出割合。たとえば、0.5に設定すると、XGBoost はデータの半分をランダムに選んで木を成長させることで、オーバーフィッティングを防ぎます。
colsample_bytree [default=1]
- 各木を作成するときの列におけるサブサンプルの割合

線形ブースター固有の変数

lambda [default=0]
- L2 正則化の重み項
alpha [default=0]
- L1 正則化の重み項

lambda_bias
- L2 正則化のバイアス項で、デフォルト値は0 (L1正則化のバイアス項は重要でないためありません)

タスク変数

objective [ default=reg:linear ]
- 学習方法を明確にします。そのオプションは以下のようになります。
- "reg:linear" --線形回帰
- "reg:logistic" --ロジスティック回帰
- "binary:logistic" --2-クラス分類向けのロジスティック回帰で、確率を出力
- "binary:logitraw" --2-クラス分類向けのロジスティック回帰で、ロジスティック回帰式に代入する前の値
- "multi:softmax" --XGBoost をソフトマックス関数を使用した多クラス分類に設定します。変数num_class (クラスの数)も設定する必要があります。
- "multi:softprob" --softmax と同じであるが、各データがどのクラスに属するかの予測確率が出力されます。
- "rank:pairwise" --順位付けをペアワイズ損失が最小になるようにXGBoost を設定します
base_score [ default=0.5 ]
- すべての例に対する初めの予測スコアでグローバルバイアスである
eval_metric [ default according to objective ]
- 検証データに対する評価基準で、デフォルトの基準はobjective によって決まります。回帰であればrmse、クラス分類であればerror、順位付けではmean average precision がデフォルトとなります。
- 選択肢は以下の通りです
- "rmse": 2乗平均平方根誤差
- "logloss": 負の対数尤度
- "error": 2-クラス分類のエラー率。(分類の誤ったケース数) / (すべてのケース数) で計算される。たとえば予測において、この評価値は0.5 よりも大きければ予測は良い例であり、0.5 よりも小さい場合には悪い例となる。
- "merror": 多クラス分類のエラー率。(誤認したケースの数) / (すべてのケース数).
- "mlogloss": 多クラスの対数損失
- "auc": Area under the curve の略でROC曲線下の面積で、性能の良さを表します
- "ndcg":Normalized Discounted Cumulative Gain の略で順位付け問題の性能評価に用いられる
- "map": Mean average precision の略
seed [ default=0 ]
- 乱数シード値

コンソール変数

以下の変数はコンソール版のxgboost にのみ適用されます(一部省略)

use_buffer [ default=1 ]
- テキストからの入力のためにバイナリバッファを作るかどうかで、たいていの場合データの読み込みのスピードが改善します

num_round
- ブースティングを行う回数
data
- トレーニングデータのパス
test:data
- 予測する用のテストデータのパス

*1:強固になるの意味は、外れ値に強くなるという意味と汎化性能が低くなるの両方の意味を込めています。